UAM Nuevas técnicas de aprendizaje automático
Nuevas técnicas de aprendizaje automático, investigadores de la Universidad Autónoma de Madrid (UAM) han explorado nuevas técnicas de aprendizaje automático basadas en procesos Gaussianos que, mediante la minimización de α-divergencias, permiten hacer predicciones más precisas. Los resultados se publican en la revista Neurocomputing.
El aprendizaje automático es una rama de la informática y la inteligencia artificial. Se basa en el entrenamiento de un modelo estadístico a partir de un conjunto de datos, de tal modo que el modelo puede luego hacer predicciones sobre nuevos datos del mismo tipo.
Por ejemplo, si tuviéramos un conjunto de datos con características de frutas (color, textura, tamaño) etiquetadas con el tipo de fruta que es cada ejemplo (piña, manzana o naranja), nuestro modelo aprendería de estos datos y podría predecir para un ejemplo que aún no está etiquetado qué tipo de fruta es en función de estas características con las que hemos entrenado el modelo.
El algoritmo de aprendizaje automático entrena un modelo para luego hacer predicciones sobre nuevos datos.
Como parte de un trabajo reciente, publicado en Neurocomputing, el Grupo de Aprendizaje Automático (GAA) de la Universidad Autónoma de Madrid (UAM) ha entrenado un tipo de modelos de aprendizaje automático llamados procesos Gaussianos, logrando predicciones aún más precisas.
Los procesos Gaussianos tienen la ventaja de que, al ser modelos Bayesianos, proporcionan una estimación de la incertidumbre asociada a las predicciones; en otras palabras, nos dicen cómo de fiables son estas predicciones.
Esto es crítico en ciertas aplicaciones en las que tomar una mala decisión puede tener consecuencias desastrosas. Por ejemplo, el software de un coche autónomo podría determinar que delante de él no hay peatones cruzando un paso de cebra y producirse un atropello porque en realidad sí los había. Si supiera que su predicción no es muy fiable, el coche podría extremar la precaución y evitar el accidente.
Clasificación multiclase y medidas de divergencia
En su trabajo, los autores consideran problemas de clasificación multiclase, es decir, problemas en los que la predicción del modelo será una etiqueta de entre un conjunto finito de un mínimo de tres elementos, como en el ejemplo de clasificar frutas mencionado anteriormente, en la que teníamos tres tipos de fruta: piñas, manzanas y naranjas.
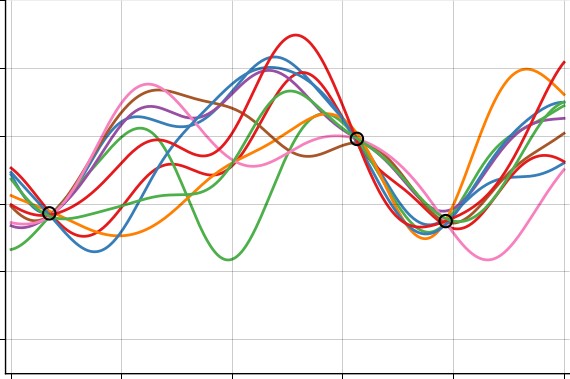
“Se puede interpretar la regla que asigna una etiqueta de clase para cada dato de entrada como una función. El algoritmo de aprendizaje consiste en calcular qué funciones son compatibles con los datos observados. Para ello se obtiene una distribución de probabilidad sobre funciones. La distribución exacta es muy complicada y debe aproximarse”, explican los autores.
“Este proceso —agregan— se lleva a cabo usando una distribución aproximada que es ajustada mediante la minimización de la divergencia de Kullback-Leibler. Esta divergencia será más pequeña cuanto mejor sea la aproximación que usemos”.
Los resultados muestran que con este tipo de modelos se puede utilizar una familia de medidas de divergencia llamadas α-divergencias, que se pueden ver como una generalización de la divergencia de Kullback-Leibler, con un parámetro α que se puede variar para cambiar la medida de divergencia.
A su vez, los autores demuestran en varios experimentos que variando el valor de este parámetro se pueden obtener predicciones más certeras que con la divergencia de Kullback-Leibler. Esto, como ya se ha mencionado, es importante para aplicaciones en las que nos interesa no solo acertar con las predicciones que se hacen, sino también conocer la incertidumbre de estas predicciones.