Un algoritmo probabilístico para optimizar soluciones complejas
Investigadores de la Escuela Politécnica Superior de la Universidad Autónoma de Madrid (EPS-UAM) han diseñado un nuevo algoritmo que ayuda a solucionar procesos que requieren la optimización de múltiples objetivos a la vez. El trabajo se publica en la revista Neurocomputing.
Muchos problemas requieren optimizar múltiples objetivos bajo restricciones, donde tanto unos como otras no tienen una expresión analítica y son costosos de evaluar. Además, las evaluaciones de los objetivos y las restricciones pueden dar resultados distintos para una misma configuración.

Eduardo Garrido Merchan
Investigadores de la Escuela Politécnica Superior de la Universidad Autónoma de Madrid (EPS-UAM) han presentado en la revista Neurocomputing un algoritmo que obtiene una solución para este tipo de problemas, con un número reducido de evaluaciones de los objetivos y las restricciones.
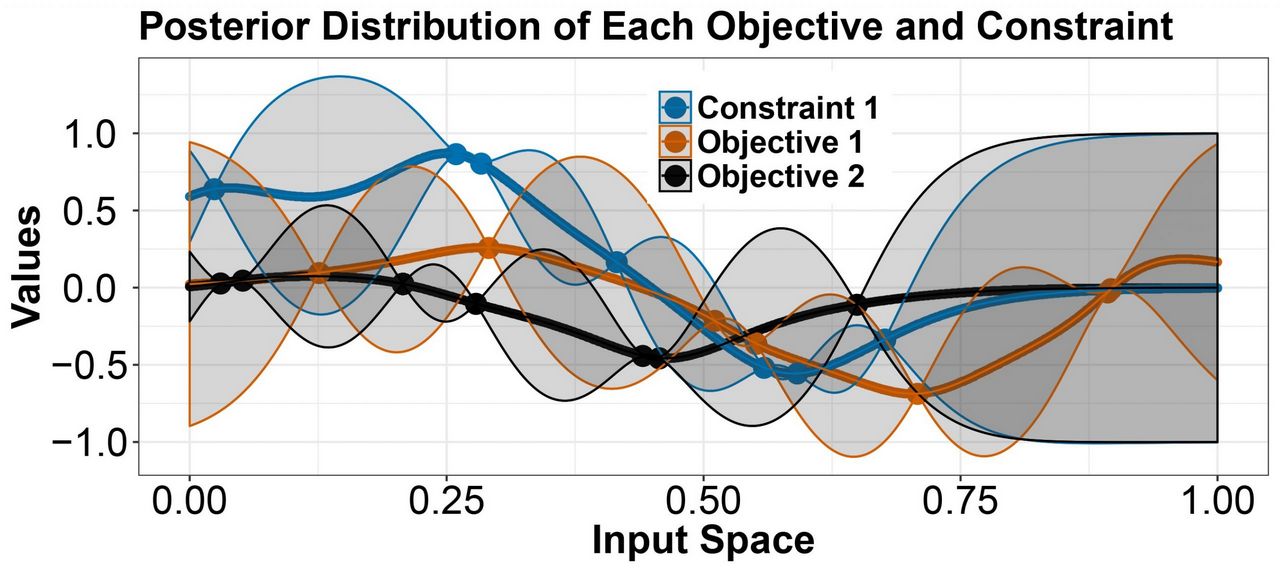
Se trata de un algoritmo de la familia bayesiana. Los algoritmos de optimización bayesiana lidian con la incertidumbre mediante modelos probabilísticos que, para una configuración de variables dada, brindan la solución más óptima y un valor de incertidumbre asociada, sin necesidad de evaluar los objetivos ni las restricciones.
“Hemos propuesto un algoritmo que es capaz de resolver de forma inteligente problemas y proponer una buena solución al terminar el proceso de optimización. Nuestro algoritmo emplea una predicción e incertidumbre junto con la teoría de la información para sugerir cual es el siguiente punto donde evaluar, tanto objetivos como restricciones, para encontrar la solución al problema en un número pequeño de pasos”, explican los autores.
Una vez realizada la evaluación, los modelos probabilísticos se actualizan y vuelven a sugerir una nueva configuración a evaluar, repitiéndose el proceso anterior. De esta manera, el algoritmo sugiere tantas configuraciones como evaluaciones posibles.

Daniel Hernández Lobato
“Cuando el presupuesto se agota, se sugiere como configuración final la que los modelos probabilísticos consideran que es la mejor dada la información que ha sido obtenida hasta el momento. Estos algoritmos, al no tener en cuenta el componente humano, son capaces de evitar prejuicios y por tanto pueden llegar a soluciones que no habrían sido tomadas en caso de no utilizarlos”, detallan los autores.
“En nuestro trabajo —agregan— exponemos un ejemplo real del empleo de este algoritmo para optimizar redes neuronales de tal forma que se garantice que el tamaño del chip que codifica la red neuronal sea inferior a 1 mm cuadrado, y que su predicción sea lo más precisa y rápida posible. Consideramos que la resolución de este tipo de tareas puede ser de gran utilidad, por ejemplo, en el campo de la medicina, las energías renovables y la búsqueda de nuevos materiales”.
Soluciones complejas algoritmo probabilístico para optimizar soluciones complejas
Supongamos que deseamos minimizar el coste de elaborar un producto industrial, pero a la vez queremos maximizar su calidad y, además, no contaminar el medio ambiente. Nos interesa entonces obtener soluciones que optimicen los tres objetivos y que cumplan las restricciones del conjunto. Pero optimizar múltiples objetivos es complejo, sobre todo porque estos suelen ser contradictorios entre sí.
En la práctica, el número de combinaciones de valores variables puede ser gigantesco, siendo muy difícil para los seres humanos considerar todas las opciones posibles. En consecuencia, es usual obtener resultados “subóptimos”, sesgados por la experiencia subjetiva y la subestimación de configuraciones potencialmente novedosas y mejores. Este sesgo humano resulta costoso cuando hay implicaciones económicas, temporales o de recursos humanos a la hora de evaluar todas las soluciones posibles.
Un ejemplo lo podemos encontrar en el automovilismo, donde en cada carrera se requiere lograr un coche con la configuración más óptima para determinada pista; por ejemplo, la orientación de las distintas piezas del coche que afectan su aerodinámica, la longitud de las marchas, el peso del automóvil, etc. Además, para obtener la evaluación correspondiente a cada configuración del coche es preciso realizar pruebas en pista o en el túnel de viento, ambas costosas. Por estas razones, sin la ayuda de un algoritmo como el que hemos desarrollado, en la práctica contamos solo con un número pequeño de evaluaciones; las que podamos acometer hasta agotar el presupuesto disponible para resolver el problema.
_____________________
Referencia bibliográfica: algoritmo probabilístico para optimizar soluciones complejas
Garrido-Merchán, E.C., Hernández-Lobato, D. (2019) Predictive Entropy Search for Multi-objective Bayesian Optimization with Constraints. Neurocomputing 361: 50-68.
UAM -Una proteína cerebral promueve la interconectividad neuronal